三円問題答え

甘美な答え

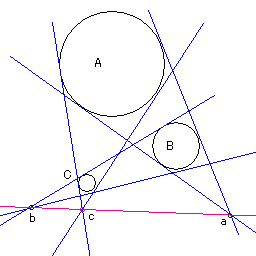
スイート教授が考えた答えです． 平面上に3個の大きさが異なる球を置き，上から見ていると考える． 球の上にもう一枚平面を置く． 平面は3個の球に接し，下の平面と直線状に交差する． 2個の球に接する円錐が3個あると考える．円錐は二つの平面とも接する． 証明終わり． 【蛇足】平面と平面が交差する部分が直線abcとなる．円の共通外接線は円錐の輪郭線と考える． うーん．確かにそうなる．

甘美な証明は苦い？

上記の証明は完全ではない．どこが完全ではないのか．

答え

上に置いた平面が3個の球に接しない場合がある．
たとえば球Cが球Aと球Bに接する円錐の輪郭線内に入っている場合である．

完全な甘美を求めて

甘美な苦味を解消せよ．

答え

1. 平面上に3個の大きさが同じ球を置き，横から見ていると考える．
2. 2個の球に接する長さが無限の円柱が3個あると考える．
3. 透視投影する．
4. 証明終わり．

【蛇足】水平線が直線abcとなる．円の共通外接線は円柱の輪郭線と考える．

これは美しい．額縁にいれて飾りたくなる

別解など

別解はないのでしょうか．ということで考えてみました．

答え

1. 平面上に3個の大きさが異なる球を置き，上から見ていると考える．
2. 3球の中心を通る平面を考える．
3. 2個の球に接する円錐が3個あると考える．円錐の頂点は二つの平面上にある．
4. 証明終わり．

【蛇足】こうすれば球の大きさが異なるので球の中心は同一直線上になく （例外もあるがその場合は円錐が一つ）平面も一意に決まる．

似たような問題

2次元図形の定理を3次元で華麗にとく，というのは他にもある．こんな問題である．

楕円とは二つの焦点との距離の和が等しい点の軌跡である． では円を一方向に引き伸ばした図形が楕円であることを証明せよ．

よかったら考えてみて下さい．
【ヒント】円を一方向に引き伸ばした図形とは円柱の斜断面のことである．