三円問題

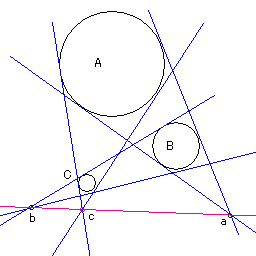
平面上に円を三つ描く．名前はA,B,Cとする．その中の二つの円の共通外接線を描く．二つの円の直径が異なる場合，二本の外接線はどこかで交差する．たとえば円Aと円Bの外接線の交点は点aとなる．円B,Cで交点bができ，円C,Aで交点cができる．この三つの交点a,b,cはなんとびっくり，同一直線上にある．
そこで問題は「この定理を証明せよ」となるのだが，パズルと銘打った以上は当然あっとびっくりする華麗な証明方法で頼みます．

これは「数学ゲームI」（マーチン・ガードナー著，日本経済新聞社,1979）に掲載されていた問題です．この本にはこう書いてあります．

この定理を，コーネル大学の工学部の教授であり，1916年になくなったスイートに見せたところ, 彼はしばらくその図をしらべて，それからいった．「うん，これはまったく自明だ...」．スイート教授のスイートな（甘美な）証明とはどんなものであったか．